Descriptive Statistics: Tools, Techniques, and Applications

Target Audience: The target audience for this Article includes students and data analysts. This guide is especially beneficial for students who are new to statistics and data analysis, providing them with foundational knowledge and practical applications of descriptive statistics.

Value Proposition: This Article on descriptive statistics will equip students with a solid understanding of key statistical concepts, measures, and graphical methods. It will enhance their ability to analyze and interpret data accurately, which is essential for making informed decisions and conducting effective research. By learning about the various measures of central tendency, dispersion, and association, students will be able to summarize and describe data sets effectively. The inclusion of practical applications and real-world examples will help students see the relevance and importance of descriptive statistics in their studies and future careers.

Key Takeaways: Descriptive statistics are a fundamental component of data analysis, providing students with a clear understanding of the characteristics and patterns within a dataset. By mastering the calculation and interpretation of measures like the mean, median, mode, range, variance, standard deviation, and correlation, students will gain valuable skills for summarizing and visualizing data. Through hands-on experience with statistical software and real-world applications, students will learn to clean data, handle outliers, and construct informative charts and plots. Importantly, students will also develop an appreciation for the assumptions, limitations, and practical considerations necessary for the accurate interpretation and application of descriptive statistics. This knowledge will empower students to make informed decisions, conduct robust research, and effectively communicate data-driven insights across various academic and professional domains.

Descriptive Statistics: An Introduction to Analyzing Data

Descriptive statistics is a branch of statistics that involves the collection, organization, analysis, and presentation of data in a meaningful way. It provides a summary of the main features of a dataset, allowing researchers and analysts to gain insights and draw conclusions from the data. Descriptive statistics plays a crucial role in data analysis, particularly in engineering fields, where data is often used to make informed decisions and solve complex problems.

Definition and Importance of Descriptive Statistics

Descriptive statistics is the process of transforming raw data into a format that is easy to understand and interpret. It involves the use of various measures, such as central tendency (mean, median, mode), measures of dispersion (range, variance, standard deviation), and measures of position (percentiles, quartiles). These measures help researchers summarize the characteristics of a dataset, identify patterns, and detect any unusual or outlying data points.

The importance of descriptive statistics in engineering cannot be overstated. Engineers often work with large datasets, and descriptive statistics provide a way to make sense of this data. By using descriptive statistics, engineers can:

1. Understand the characteristics of a dataset: Descriptive statistics allows engineers to understand the distribution of data, identify the central tendency, and measure the variability within the dataset.
2. Identify patterns and trends: By analyzing the measures of central tendency and dispersion, engineers can identify patterns and trends in the data, which can be used to make informed decisions and predictions.
3. Communicate findings: Descriptive statistics provides a concise and clear way to communicate the results of data analysis to stakeholders, such as project managers, clients, or other engineers.
4. Improve decision-making: By understanding the characteristics of a dataset, engineers can make more informed decisions and develop better solutions to engineering problems.

Descriptive Statistics: The Crucial Role in Data Analysis

Descriptive statistics plays a crucial role in the data analysis process, which typically involves the following steps:

1. Data collection: Engineers collect data from various sources, such as experiments, simulations, or real-world observations.
2. Data cleaning and preprocessing: The collected data is cleaned and preprocessed to remove any errors, inconsistencies, or missing values.
3. Exploratory data analysis: Descriptive statistics is used to explore the dataset and gain insights into its characteristics. This includes calculating measures of central tendency, dispersion, and position, as well as creating visualizations such as histograms, scatter plots, and box plots.
4. Hypothesis testing: Descriptive statistics is used to test hypotheses about the dataset, such as whether two groups have significantly different means or whether a variable is normally distributed.
5. Modeling and prediction: The insights gained from descriptive statistics can be used to develop models and make predictions about future events or scenarios.

By understanding the role of descriptive statistics in data analysis, engineering students can develop a strong foundation for working with data in their future careers. They can learn how to use descriptive statistics to explore datasets, identify patterns and trends, and communicate their findings to stakeholders. Additionally, by mastering the concepts of descriptive statistics, engineering students can develop critical thinking and problem-solving skills that are essential for success in their field.

Measures of Central Tendency

1. Mean

Definition: The mean, commonly known as the average, is the sum of all the values in a dataset divided by the number of values.

Formula: Mean(μ)=∑i=1nxin\text{Mean} (\mu) = \frac{\sum_{i=1}^{n} x_i}{n}Mean(μ)=n∑i=1n​xi​​ where xix_ixi​ represents each value in the dataset and nnn is the number of values.

Example: Consider the dataset: 4, 8, 6, 5, 3, 7 Mean=4+8+6+5+3+76=336=5.5\text{Mean} = \frac{4 + 8 + 6 + 5 + 3 + 7}{6} = \frac{33}{6} = 5.5Mean=64+8+6+5+3+7​=633​=5.5

When to Use:

• The mean is useful when the dataset has no extreme outliers, as it takes all values into account.
• It is used in scenarios where each value in the dataset contributes equally to the overall average, such as calculating average grades or average temperatures.

Interpretation:

• The mean provides a central value around which the data points are distributed.
• It is sensitive to outliers, which can skew the mean higher or lower.

2. Median

Definition: The median is the middle value in a dataset when the values are arranged in ascending or descending order. If there is an even number of observations, the median is the average of the two middle values.

Example: Consider the dataset: 4, 8, 6, 5, 3, 7 Ordered dataset: 3, 4, 5, 6, 7, 8 Since there is an even number of values, the median is the average of the third and fourth values: Median=5+62=5.5\text{Median} = \frac{5 + 6}{2} = 5.5Median=25+6​=5.5

When to Use:

• The median is useful when the dataset has outliers or is skewed, as it is not affected by extreme values.
• It is often used in income data, real estate prices, and other financial metrics where outliers can distort the mean.

Interpretation:

• The median represents the middle value, providing a better central tendency measure in skewed distributions.
• It divides the dataset into two equal parts, with half the values below the median and half above.

3. Mode

Definition: The mode is the value that appears most frequently in a dataset. A dataset can have one mode, more than one mode, or no mode at all.

Example: Consider the dataset: 4, 8, 6, 5, 3, 7, 5 The value 5 appears twice, while all other values appear only once. Mode=5\text{Mode} = 5Mode=5

When to Use:

• The mode is useful for categorical data where we wish to know the most common category.
• It is used in situations where the most frequent occurrence of a value is of interest, such as in market research to identify the most popular product.

Interpretation:

• The mode indicates the most common value in a dataset.
• In a dataset with no repeating values, there is no mode.

Practical Insights and Takeaways

• Choosing the Right Measure:
  • Mean: Use when you need a precise central value and the data is symmetrically distributed without outliers.
  • Median: Use when dealing with skewed distributions or when outliers are present.
  • Mode: Use for categorical data or to find the most common value in the dataset.
• Examples in Real-Life Contexts:
  • Mean: Average test scores in a class.
  • Median: Median household income in a country.
  • Mode: Most common shoe size sold in a store.

By understanding and appropriately applying the mean, median, and mode, students can accurately describe and analyze datasets, making informed decisions based on the nature of the data.

Measures of Dispersion: Understanding the Spread of Data

Measures of dispersion are statistical measures that quantify the spread or variability of a dataset. These measures are essential in understanding the distribution of data and how it is spread out around the central tendency. In the context of engineering, measures of dispersion can provide valuable insights into the consistency and reliability of data, which is crucial for making informed decisions and developing effective solutions. Here, we explore key measures of dispersion: Range, Variance, Standard Deviation, Interquartile Range (IQR), and Coefficient of Variation (CV).

1. Range

Definition: The range is the simplest measure of dispersion, calculated as the difference between the highest and lowest values in a data set.

Formula: Range=Maximum value−Minimum value\text{Range} = \text{Maximum value} – \text{Minimum value}Range=Maximum value−Minimum value

Example: Consider the data set: 3, 7, 8, 5, 12, 14, 21, 13, 18

• Maximum value = 21
• Minimum value = 3
• Range = 21 – 3 = 18

Practical Insight: While easy to compute, the range is sensitive to outliers and does not provide information about the distribution of values between the extremes.

2. Variance

Definition: Variance measures the average squared deviation of each number from the mean of the data set. It provides a more comprehensive view of dispersion.

Formula: For a population: σ2=∑(xi−μ)2N\sigma^2 = \frac{\sum (x_i – \mu)^2}{N}σ2=N∑(xi​−μ)2​

For a sample: s2=∑(xi−xˉ)2n−1s^2 = \frac{\sum (x_i – \bar{x})^2}{n-1}s2=n−1∑(xi​−xˉ)2​

Example: For the data set: 3, 7, 8, 5, 12

• Mean ( xˉ\bar{x}xˉ ) = (3 + 7 + 8 + 5 + 12) / 5 = 7
• Squared deviations: (3-7)², (7-7)², (8-7)², (5-7)², (12-7)² = 16, 0, 1, 4, 25
• Variance: (16 + 0 + 1 + 4 + 25) / (5 – 1) = 46 / 4 = 11.5

Practical Insight: Variance is in squared units of the original data, making it less interpretable than standard deviation. However, it is foundational for other statistical calculations.

3. Standard Deviation

Definition: Standard deviation is the square root of variance, providing a measure of dispersion in the same units as the data.

Formula: σ=σ2\sigma = \sqrt{\sigma^2}σ=σ2​ s=s2s = \sqrt{s^2}s=s2​

Example: Continuing from the variance example above:

• Standard Deviation = 11.5≈3.39\sqrt{11.5} \approx 3.3911.5​≈3.39

Practical Insight: Standard deviation is widely used due to its intuitive interpretation and the same units as the original data, making it easier to understand and compare.

4. Interquartile Range (IQR)

Definition: The IQR measures the spread of the middle 50% of a data set, calculated as the difference between the third quartile (Q3) and the first quartile (Q1).

Formula: IQR=Q3−Q1\text{IQR} = Q3 – Q1IQR=Q3−Q1

Example: For the data set: 5, 7, 8, 12, 14

• Ordered data: 5, 7, 8, 12, 14
• Q1 (first quartile) = 7
• Q3 (third quartile) = 12
• IQR = 12 – 7 = 5

Practical Insight: The IQR is resistant to outliers and provides a focused view of data dispersion, especially useful in box plots.

5. Coefficient of Variation (CV)

Definition: The CV expresses the standard deviation as a percentage of the mean, useful for comparing the degree of variation between different data sets.

Formula: CV=(σμ)×100%\text{CV} = \left( \frac{\sigma}{\mu} \right) \times 100\%CV=(μσ​)×100%

Example: For a data set with a mean (μ\muμ) of 50 and a standard deviation (σ\sigmaσ) of 5:

• CV = (5 / 50) × 100% = 10%

Practical Insight: CV is particularly useful when comparing the variability of data sets with different units or widely different means.

Understanding measures of dispersion is crucial for interpreting the variability and reliability of data. While range, variance, standard deviation, IQR, and CV each provide unique insights, together they form a comprehensive toolkit for data analysis.

By mastering these concepts, students can better analyze data sets, identify patterns, and make informed decisions based on statistical evidence.

Frequency Distributions

Definition and Construction of Frequency Distributions

A frequency distribution is a way to organize data to show how often each value (or range of values) occurs. It provides a visual summary of the data, making it easier to see patterns and draw conclusions.

Steps to Construct a Frequency Distribution:

1. Collect Data: Gather the data you need to analyze.
2. Create Intervals (if necessary): If your data set is large, divide it into intervals (also known as bins or classes).
3. Tally the Frequencies: Count how many data points fall into each interval or how many times each unique value occurs.
4. Create a Table: Organize the intervals and their corresponding frequencies into a table.

Example: Suppose you have the following data on the ages of a group of people: 18, 22, 25, 25, 28, 30, 30, 30, 32, 35, 36, 36, 38, 40, 42.

Age Interval	Frequency
18-22	2
23-27	1
28-32	6
33-37	3
38-42	3

Histograms and Frequency Polygons

Histograms

A histogram is a type of bar chart that represents the frequency distribution of a data set. Each bar represents the frequency (count) of data points within an interval. The height of each bar reflects the frequency.

Example: Using the age data above, we can create a histogram:

• The x-axis represents the age intervals.
• The y-axis represents the frequency of each interval.

Frequency Polygons

A frequency polygon is a graphical device for understanding the shapes of distributions. It is constructed by plotting points above the midpoints of each interval at a height corresponding to the frequency and connecting the points with straight lines.

Example: Using the same age data, plot points at the midpoints of each interval (e.g., 20, 25, 30, 35, 40) and connect them with lines.

Cumulative Frequency Distributions

A cumulative frequency distribution shows the cumulative total of the frequencies up to a certain point. It is useful for understanding the distribution of data over a range of values.

Steps to Construct a Cumulative Frequency Distribution:

1. Create the Frequency Distribution Table: Start with the frequency distribution table.
2. Calculate the Cumulative Frequency: Add the frequency of each interval to the sum of the frequencies of all previous intervals.

Example: Continuing with our age data:

Age Interval	Frequency	Cumulative Frequency
18-22	2	2
23-27	1	3
28-32	6	9
33-37	3	12
38-42	3	15

Cumulative Frequency Graph (Ogive)

A cumulative frequency graph, or ogive, is a line graph that represents the cumulative frequencies for the class intervals.

• The x-axis represents the upper boundary of each interval.
• The y-axis represents the cumulative frequency.

Example: Using the cumulative frequency data above, plot the cumulative frequencies at the upper boundaries of the intervals (e.g., 22, 27, 32, 37, 42) and connect them with lines.

Practical Insights and Takeaways

• Understanding Data Distribution: Frequency distributions help in understanding how data is spread out. Histograms and frequency polygons provide visual clarity, making it easier to identify patterns, trends, and outliers.
• Making Comparisons: They allow for easy comparison between different sets of data.
• Identifying Data Trends: Cumulative frequency distributions and ogives are particularly useful for identifying trends over time or across categories.

By using frequency distributions, histograms, and frequency polygons, students can gain deeper insights into the nature of their data, making it easier to perform further statistical analysis and draw meaningful conclusions.

Graphical Methods in Descriptive Statistics

Graphical methods are powerful tools in descriptive statistics, allowing us to visualize data in a way that is easy to understand and interpret. This article will cover four essential graphical methods: bar charts, pie charts, box plots, and scatter plots. Each method will be explained with practical insights and examples to help students grasp their use and importance.

Bar Charts

Bar charts are used to represent categorical data with rectangular bars. Each bar’s height or length corresponds to the frequency or value of the category it represents.

Example: Suppose we have data on the favorite fruits of a group of students:

• Apples: 10 students
• Bananas: 15 students
• Oranges: 8 students
• Grapes: 12 students

We can create a bar chart to visualize this data:

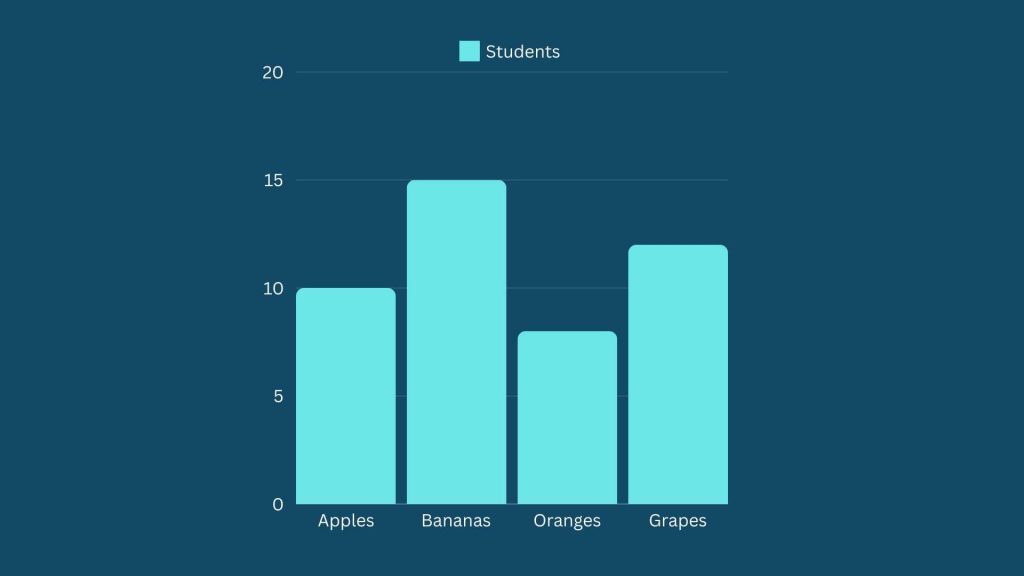
Key Points:

• Bars can be vertical or horizontal.
• The height or length of the bars represents the frequency or count of each category.
• It is useful for comparing different categories.

Bar charts are great for comparing the popularity of different categories, such as the example of the favorite fruit. They help quickly identify which category is the most or least popular.

Pie Charts

Pie charts represent data as slices of a circle, where each slice corresponds to a category’s proportion of the total.

Example: Using the same fruit data, we can create a pie chart:

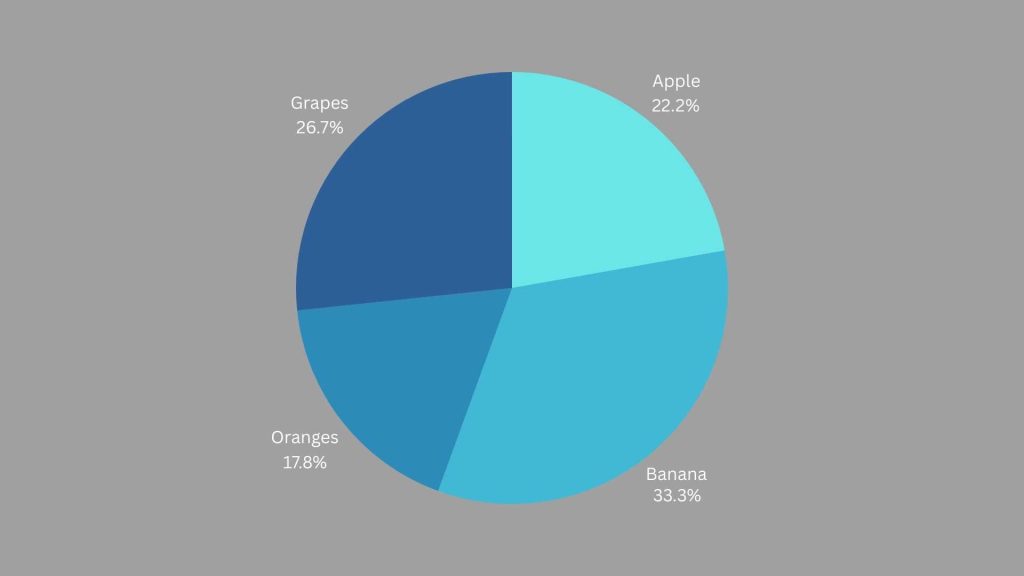
Key Points:

• Each slice represents a category’s proportion of the total.
• Useful for showing the relative proportions of different categories.
• Best for displaying a small number of categories.

Pie charts are effective for showing the part-to-whole relationship. In our fruit example, they clearly illustrates the proportion of students who prefer each fruit.

Box Plots (Box-and-Whisker Plots)

Box plots display the distribution of data based on a five-number summary: minimum, first quartile (Q1), median, third quartile (Q3), and maximum.

Example: Consider the following data on test scores: 55, 60, 65, 70, 75, 80, 85, 90, 95, 100. A box plot for this data looks like this:

   55 ┼─────┼
       60 ┼─────┼
       65 ┼─────┼
       70 ┼─────┼
       75 ┼─────┼
       80 ┼─────┼
       85 ┼─────┼
       90 ┼─────┼
       95 ┼─────┼
      100 ┼─────┼
           └─────┘
  Minimum: 55
  Q1: 67.5
  Median: 77.5
  Q3: 87.5
  Maximum: 100

In a box plot:

• The line inside the box represents the median (Q2).
• The box spans the interquartile range (Q1 to Q3), showing the middle 50% of the data.
• The whiskers extend to the minimum and maximum values within 1.5 times the interquartile range.
• Outliers are shown as individual points beyond the whiskers.

Key Points:

• The box represents the interquartile range (IQR), where 50% of the data lies.
• The line inside the box indicates the median.
• Whiskers extend to the minimum and maximum values within 1.5*IQR from Q1 and Q3.
• Outliers may be plotted as individual points.

Box plots are excellent for identifying the spread and skewness of data, as well as outliers. In our test scores example, they help us see the distribution of scores and any potential outliers.

Scatter Plots

Scatter plots are used to display the relationship between two numerical variables by plotting data points on a two-dimensional plane.

Example: Let’s say we have data on students’ study hours and their test scores:

Study Hours	Test Score
2	60
3	65
4	70
5	75
6	80

We can create a scatter plot to visualize this relationship:

Key Points:

• Each point represents an observation.
• Useful for identifying relationships or correlations between variables.
• The pattern of points can indicate different types of relationships (e.g., linear, non-linear).

Scatter plots are powerful tools for exploring correlations. In our study hours and test scores example, the scatter plot helps us see that there is a positive relationship between the two variables: as study hours increase, test scores tend to increase.

Understanding and using these graphical methods can greatly enhance your ability to analyze and interpret data. Bar charts and pie charts are excellent for categorical data, while box plots and scatter plots provide deeper insights into numerical data. By mastering these tools, you’ll be better equipped to communicate your data findings effectively.

Skewness and Kurtosis: Understanding the Shapes of Distributions

Skewness

Definition and Interpretation:

Skewness is a measure of the asymmetry of the probability distribution of a real-valued random variable about its mean. It tells us about the direction and the extent of skew (deviation from the normal distribution) in the dataset.

• Positive Skew (Right Skew): When the right tail (larger values) is longer or fatter than the left tail (smaller values). The mean is greater than the median.
• Negative Skew (Left Skew): When the left tail (smaller values) is longer or fatter than the right tail (larger values). The median is greater than the mean.
• Zero Skew (Symmetric): When the tails on both sides of the mean are balanced, and it resembles a bell curve. The mean and median are roughly equal.

Calculation:

Skewness can be calculated using the formula:

Skewness=(n−1)(n−2)n​∑i=1n​(sxi​−xˉ​)3

Where:

• n = number of observations
• xi = value of the i^{th} observation
• xˉ = mean of the observations
• s = standard deviation of the observations

Implications:

• Financial Data: Positive skewness might indicate a larger number of returns that are higher than average.
• Quality Control: Negative skewness might suggest a majority of processes are running more efficiently than average.

Example:

Consider the test scores of two classes:

• Class A: [55, 60, 65, 70, 75, 80, 85, 90, 95]
• Class B: [65, 70, 75, 80, 85, 90, 95, 100, 105]

Class A is negatively skewed because more students scored below the mean, whereas Class B is positively skewed. After all, more students scored above the mean.

Kurtosis

Definition and Interpretation:

Kurtosis is a measure of the “tailedness” of the probability distribution of a real-valued random variable. It indicates how heavily the tails of the distribution differ from the tails of a normal distribution.

• Leptokurtic (Positive Kurtosis): Distributions with positive kurtosis have heavy tails and a sharp peak, indicating more data is in the tails and around the mean.
• Platykurtic (Negative Kurtosis): Distributions with negative kurtosis have light tails and a flat peak, indicating less data in the tails and around the mean.
• Mesokurtic (Zero Kurtosis): Distributions with kurtosis similar to the normal distribution, indicating moderate tails and peaks.

Calculation:

Kurtosis can be calculated using the formula:

Kurtosis=(n−1)(n−2)(n−3)n(n+1)​∑i=1n​(sxi​−xˉ​)4−(n−2)(n−3)3(n−1)2​

Where:

• n = number of observations
• xi​ = value of the i^{th} observation
• xˉ = mean of the observations
• s = standard deviation of the observations

Implications:

• Risk Management: Higher kurtosis indicates higher risk due to extreme values.
• Insurance: Leptokurtic distributions might suggest a higher probability of extreme claims.

Example:

Consider two datasets of returns on investments:

• Dataset A: [2, 2, 2, 2, 2, 2, 20]
• Dataset B: [2, 2, 2, 2, 2, 2, 2]

Dataset A has a high kurtosis (leptokurtic) due to the extreme value (20), indicating a higher risk of extreme returns. Dataset B has low kurtosis (platykurtic), indicating less risk of extreme values.

• Analyzing Skewness and Kurtosis Together: By analyzing both skewness and kurtosis, we can get a more comprehensive understanding of the data’s distribution. For instance, a dataset can be positively skewed with high kurtosis, indicating a large number of high outliers.
• Adjusting Strategies: In finance, portfolios might be adjusted based on skewness and kurtosis to manage risks better.
• Quality Control Adjustments: Manufacturing processes can be adjusted by analyzing these metrics to ensure consistency and quality.

Understanding skewness and kurtosis provides valuable insights into the nature of the data distribution. These metrics help in identifying the asymmetry and the tails’ heaviness, enabling better decision-making and risk management.

By visualizing and calculating these measures, students can gain practical insights into their data, allowing them to draw more accurate conclusions and improve their analytical skills.

Measures of Association

Understanding the relationship between two variables is crucial in data analysis. Measures of association, such as covariance and the correlation coefficient, help quantify the strength and direction of these relationships. Let’s explore these concepts in detail with practical insights and examples.

Covariance

Covariance measures how much two random variables change together. If the greater values of one variable correspond with the greater values of another variable, and the same holds for the lesser values, the covariance is positive. Conversely, if greater values of one variable correspond with lesser values of another, the covariance is negative.

Formula:

(X, Y)=n1​∑i=1n​(Xi​−Xˉ)(Yi​−Yˉ)

Where:

• X and Y are the variables
• Xi​ and Yi​ are the individual sample points
• Xˉ and Yˉ are the means of X and Y
• n is the number of data points

Example:

Consider the heights and weights of five individuals:

Height (X)	Weight (Y)
160	55
165	60
170	65
175	70
180	75

1. Calculate the means of X and Y: 

Xˉ=5160+165+170+175+180​ / 5=170

Yˉ=555+60+65+70+75​ / 5=65

2. Calculate the covariance: 

Cov(X,Y)=1/5​[(160−170)(55−65)+(165−170)(60−65)+(170−170)(65−65)+(175−170)(70−65)+(180−170)(75−65)]

Cov(X,Y)=1/5​[(−10)(−10)+(−5)(−5)+(0)(0)+(5)(5)+(10)(10)]

Cov(X,Y)=1/5​[100+25+0+25+100]=5250​=50

The positive covariance indicates that as height increases, weight tends to increase as well.

Correlation Coefficient (Pearson Correlation)

Pearson correlation coefficient is a normalized measure of covariance that indicates both the strength and direction of the linear relationship between two variables. It ranges from -1 to 1.

Formula: r=σX​σY​Cov(X,Y)​

Where:

• Cov(X, Y) is the covariance of X and Y
• σX​ and σY​ are the standard deviations of X and Y

Example:

Using the previous height and weight data:

1. Calculate the standard deviations: σX​=51​∑i=15​(Xi​−Xˉ)2​=51​[(−10)2+(−5)2+(0)2+(5)2+(10)2]​=51​[100+25+0+25+100]​=50​≈7.07

σY​=51​∑i=15​(Yi​−Yˉ)2​=51​[(−10)2+(−5)2+(0)2+(5)2+(10)2]​=50​≈7.07

2. Calculate the Pearson correlation coefficient: 

r=50/7.07×7.07 ​=50/50​=1

The correlation coefficient r=1r = 1r=1 indicates a perfect positive linear relationship between height and weight.

Interpretation of Correlation Strength

The value of the Pearson correlation coefficient (rrr) provides insight into the strength and direction of the linear relationship between two variables:

• r=1r = 1r=1: Perfect positive correlation
• r=−1r = -1r=−1: Perfect negative correlation
• 0.7≤∣r∣<10.7 \leq |r| < 10.7≤∣r∣<1: Strong correlation
• 0.4≤∣r∣<0.70.4 \leq |r| < 0.70.4≤∣r∣<0.7: Moderate correlation
• 0.2≤∣r∣<0.40.2 \leq |r| < 0.40.2≤∣r∣<0.4: Weak correlation
• ∣r∣<0.2|r| < 0.2∣r∣<0.2: Very weak or no correlation

Practical Insight:

Understanding the correlation between variables can help in various practical scenarios:

1. Marketing: A strong positive correlation between advertising spend and sales revenue can indicate that increased advertising leads to higher sales.
2. Finance: A negative correlation between interest rates and stock prices can help investors make informed decisions about their portfolios.
3. Healthcare: Identifying the correlation between lifestyle factors and health outcomes can guide public health interventions.

Visualization:

Visualizing the relationship between variables helps in better understanding their association. Below are some examples of scatter plots demonstrating different correlation strengths:

• Perfect Positive Correlation (r=1r = 1r=1):
• Strong Positive Correlation (r=0.8r = 0.8r=0.8):
• No Correlation (r=0r = 0r=0):

Understanding these concepts and how to interpret the strength of the relationship between variables is essential for analyzing data and drawing meaningful conclusions.

Descriptive Statistics Based on the Shape of the Data

Skewness and Kurtosis

Understanding the shape of data distributions is crucial in descriptive statistics. Two important measures that describe this shape are skewness and kurtosis.

Skewness measures the asymmetry of the data distribution. If the data is symmetrically distributed, skewness will be close to zero. Positive skewness indicates a distribution with a long right tail, while negative skewness indicates a distribution with a long left tail.

• Example: Consider the following set of test scores: 55, 60, 65, 70, 75, 80, 85, 90, 95, 100. If most students scored between 55 and 75 with few high scores, the distribution is positively skewed.

Kurtosis measures the “tailedness” of the distribution. A high kurtosis indicates a distribution with heavy tails and a sharp peak, while a low kurtosis indicates a distribution with light tails and a flatter peak.

• Example: In the same set of test scores, if most scores are clustered around the mean with few extreme values, the distribution has low kurtosis. Conversely, if there are many extreme values, the distribution has high kurtosis.

Univariate vs. Bivariate Statistics

Univariate Analysis

Univariate analysis involves analyzing a single variable to describe its main features, such as central tendency (mean, median, mode) and dispersion (range, variance, standard deviation).

• Example: Analyzing the test scores of a class (mean score, median score, range of scores).

Key measures include:

• Mean: Average score.
• Median: Middle score when arranged in order.
• Mode: Most frequent score.
• Range: Difference between highest and lowest scores.
• Variance and Standard Deviation: Measure of how spread out the scores are around the mean.

Bivariate Analysis

Bivariate analysis involves analyzing the relationship between two variables. This analysis can help identify correlations and dependencies between the variables.

• Example: Analyzing the relationship between study time and test scores.

Key measures include:

• Scatter Plots: Visual representation of the relationship between two variables.
• Covariance: Measure of how two variables change together.
• Correlation Coefficient (Pearson’s r): Measure of the strength and direction of the linear relationship between two variables.

Explanation of Univariate and Bivariate Analysis

Univariate Analysis:

• Purpose: To summarize and find patterns in a single variable.
• Applications: Descriptive statistics, and data visualization (histograms, box plots).
• Example: Analyzing the distribution of ages in a population using a histogram.

Bivariate Analysis:

• Purpose: To explore the relationship between two variables and understand how they interact.
• Applications: Regression analysis, correlation analysis.
• Example: Examining how hours of study impact exam scores using a scatter plot and calculating the correlation coefficient.

Practical Insights and Examples

Univariate Analysis Example

Imagine you have a dataset of students’ test scores:

Scores: 55, 60, 65, 70, 75, 80, 85, 90, 95, 100

1. Mean: (55 + 60 + 65 + 70 + 75 + 80 + 85 + 90 + 95 + 100) / 10 = 77.5
2. Median: Middle value (sorted): 77.5
3. Mode: No repeating values (no mode).
4. Range: 100 – 55 = 45
5. Standard Deviation: Calculate how each score deviates from the mean.

Bivariate Analysis Example

Now, consider you have data on hours studied and corresponding test scores:

Hours Studied: 2, 3, 5, 7, 9

Test Scores: 50, 55, 70, 85, 95

1. Scatter Plot: Plot hours studied (x-axis) against test scores (y-axis).
2. Covariance: Measure the directional relationship between hours studied and test scores.
3. Correlation Coefficient: Calculate Pearson’s r to determine the strength and direction of the linear relationship.

In this example, a positive correlation would indicate that as study hours increase, test scores tend to increase.

By understanding these concepts, students can better analyze data and make informed decisions based on statistical insights.

Practical Applications of Descriptive Statistics

Descriptive statistics play a crucial role across various domains, offering insights into data that help in understanding patterns, making informed decisions, and solving real-world problems. Here are some practical applications across different fields:

Business

In business, descriptive statistics are used extensively to analyze market trends, consumer behavior, and financial performance:

• Market Analysis: Retailers use descriptive statistics to analyze sales data by region, product category, or customer segment to identify trends and optimize inventory management.
• Financial Reporting: Companies use measures like mean and standard deviation to summarize financial data, such as quarterly revenues or expenses, to assess performance and forecast future outcomes.

Healthcare

Descriptive statistics are vital in healthcare for understanding patient demographics, treatment outcomes, and epidemiological trends:

• Patient Demographics: Hospitals use descriptive statistics to summarize patient data, such as age distributions or diagnoses, to allocate resources effectively.
• Clinical Trials: Researchers use descriptive statistics to summarize the efficacy of treatments, presenting results such as mean improvements in health metrics or distributions of side effects.

Social Sciences

In social sciences, descriptive statistics help researchers understand human behavior, societal trends, and demographic shifts:

• Survey Analysis: Pollsters and social scientists use descriptive statistics to analyze survey responses, summarizing data on public opinion or behavior patterns.
• Educational Research: Descriptive statistics are used to analyze student performance data, such as exam scores or graduation rates, to evaluate educational programs’ effectiveness.

Descriptive statistics provide a foundational toolset for analyzing and interpreting data across diverse fields. By summarizing large datasets into manageable insights, they enable professionals to make informed decisions, identify trends, and address challenges effectively. Whether in business, healthcare, or social sciences, understanding and applying descriptive statistics empower researchers and practitioners to extract meaningful information and drive impactful outcomes.

By integrating practical examples and visual aids, students can grasp the relevance of descriptive statistics in real-world scenarios, enhancing their understanding and application skills significantly. 

Data Cleaning and Preprocessing for Descriptive Statistics

Importance of Data Cleaning in Preparing for Descriptive Analysis

Data cleaning is a crucial step in the data analysis process, especially when preparing for descriptive statistics. Its primary goal is to ensure that data is accurate, complete, and ready for analysis. Here’s why data cleaning is essential:

1. Accuracy and Reliability: Clean data ensures that the descriptive statistics accurately reflect the characteristics of the dataset, minimizing errors and misleading insights.
2. Consistency: Consistent data formats and values across the dataset are necessary for reliable statistical calculations.
3. Improved Insights: Properly cleaned data allows analysts to focus on interpreting results rather than correcting errors during analysis.

Techniques for Handling Outliers and Missing Data

Handling Outliers

Outliers are data points that significantly differ from other observations in a dataset. They can distort statistical analyses if not properly managed. Here are common techniques to handle outliers:

1. Identifying Outliers: Use statistical methods like the IQR (Interquartile Range) or z-score to identify outliers.
   Example: Consider a dataset of exam scores where most scores cluster around 70-80, but a few students scored unusually high (e.g., 95). These high scores may be outliers.
2. Treatment Options:
   • Removing Outliers: Exclude outlier values from the dataset if they are likely errors or do not represent typical behavior.
     Example: If a sensor reading shows a physically impossible and unusually high temperature, it might be removed from the dataset.
   • Transforming Data: Apply transformations (e.g., logarithmic transformation) to reduce the impact of outliers on statistical analyses.
     Example: In income data where a few individuals earn exceptionally high salaries, applying a logarithmic transformation can normalize the distribution.

Handling Missing Data

Missing data can arise due to various reasons such as non-response in surveys or technical issues during data collection. Effective handling of missing data ensures the completeness and accuracy of analysis. Techniques include:

1. Identifying Missing Data: Examine the dataset to identify where data is missing (e.g., using summary statistics or visualization).
   Example: In a survey dataset, missing values in responses to specific questions can be identified.
2. Treatment Options:
   • Deleting Rows or Columns: Remove observations or variables with a significant amount of missing data if they do not affect the overall analysis.
     Example: If a survey response is missing more than 50% of its values, that entire response may be excluded from analysis.
   • Imputation: Estimate missing values based on existing data using statistical methods such as mean, median, or predictive models.
     Example: Replace missing age values in a dataset with the mean age of respondents.

Example Scenario: Consider a dataset of monthly sales figures for a retail store. After preliminary analysis, it’s observed that some months have unusually low sales figures. Upon closer inspection, it was found that these low figures were due to data entry errors where zeros were mistakenly entered instead of actual sales numbers. By cleaning the data to correct these errors, the descriptive statistics (such as mean monthly sales, variability, etc.) provide a more accurate reflection of the store’s performance.

Visualization: Below is an example of how outliers can visually distort data and the importance of cleaning them for accurate analysis.

In conclusion, data cleaning is not just about preparing data for analysis but ensuring that the insights drawn from descriptive statistics are reliable and actionable. By effectively handling outliers and missing data, analysts can uncover meaningful patterns and trends that drive informed decision-making.

Tools and Software for Descriptive Statistics

Descriptive statistics play a crucial role in analyzing and summarizing data to extract meaningful insights. Here’s an overview of popular statistical software tools used for performing descriptive analysis, tailored for engineering students seeking practical insights.

1. Excel

Features:

• User-Friendly Interface: Excel provides a familiar spreadsheet environment suitable for beginners.
• Basic Statistical Functions: Built-in functions like AVERAGE, MEDIAN, MODE, STDEV, etc., simplify calculations of measures of central tendency and dispersion.
• Charts and Graphs: Supports the creation of histograms, scatter plots, and other graphical representations.
• Data Management: Handles large datasets efficiently with sorting, filtering, and pivot tables.

Capabilities:

• Excel is adept at handling basic descriptive statistics tasks such as calculating means, medians, and standard deviations.
• It offers quick data visualization options to understand data distributions and trends.
• Excel’s integration with other Microsoft products allows for seamless data import/export and collaboration.

Practical Insight:

• Engineering students can leverage Excel for initial data exploration and quick statistical summaries.
• Understanding limitations in handling large datasets and advanced statistical techniques can guide when to transition to more robust tools.

2. SPSS (Statistical Package for the Social Sciences)

Features:

• Comprehensive Statistical Analysis: SPSS offers an extensive range of statistical procedures beyond basic descriptive statistics.
• Data Visualization: Supports the creation of customizable charts and graphs to explore data visually.
• Syntax and GUI Integration: Allows both point-and-click operations and advanced scripting for complex analyses.

Capabilities:

• SPSS excels in handling large datasets and performing complex statistical analyses such as ANOVA, regression, and factor analysis.
• Provides robust reporting capabilities with options to export results to other formats.

Practical Insight:

• Engineering students can use SPSS for advanced statistical modeling and hypothesis testing beyond simple descriptive statistics.
• Familiarity with SPSS can enhance the analytical skills required for engineering research and data-driven decision-making.

3. R

Features:

• Open-Source: R is free to use and has a vast community contributing to its development.
• Extensive Statistical Libraries: The CRAN repository offers numerous packages for various statistical analyses.
• Graphics and Visualization: Provides advanced plotting capabilities for creating publication-quality graphs.

Capabilities:

• R is highly flexible for custom analyses and complex statistical modeling.
• Supports reproducible research with scripts and integrates well with LaTeX for academic publications.

Practical Insight:

• Engineering students can benefit from R’s capabilities in advanced statistical modeling, machine learning, and data visualization.
• Learning R enhances programming skills and prepares students for analytical roles in engineering and research fields.

4. Python Libraries (e.g., NumPy, Pandas, Matplotlib, Seaborn)

Features:

• Versatility: Python is a general-purpose programming language with powerful libraries dedicated to data analysis.
• Efficiency: NumPy for numerical computations, Pandas for data manipulation, and Matplotlib/Seaborn for visualization.
• Integration: Easily integrates with other libraries and tools for machine learning and data science workflows.

Capabilities:

• Python libraries provide a comprehensive toolkit for data cleaning, preprocessing, and analysis.
• Enables integration of statistical analysis with machine learning models and other engineering applications.

Practical Insight:

• Python’s popularity in data science makes it a valuable skill for engineering students entering industries where data-driven decisions are crucial.
• Learning Python alongside statistical libraries equips students with versatile tools for tackling diverse engineering data challenges.

Understanding the capabilities and features of these tools empowers engineering students to choose the right tool based on their analytical needs and career goals. From basic statistical calculations in Excel to advanced modeling in R and Python, each tool offers unique advantages that can significantly enhance data analysis skills in engineering practice.

Limitations and Considerations of Descriptive Statistics

Descriptive statistics are essential tools for summarizing and interpreting data in a meaningful way. However, they come with certain limitations and assumptions that engineers should be aware of to ensure accurate analysis and interpretation.

Limitations of Descriptive Statistics:

1. Sensitivity to Outliers: Descriptive statistics such as the mean and standard deviation can be heavily influenced by outliers in the data, leading to skewed results.
2. Dependence on Data Distribution: Many descriptive statistics assume a specific distribution of data (often normal distribution). Deviations from this assumption can affect the validity of the results.
3. Limited Insights into Causality: Descriptive statistics describe relationships and patterns in data but do not establish causation. Understanding causality requires further analysis and experimentation.
4. Inability to Handle Missing Data: Most descriptive techniques require complete data sets. Missing data can distort results or require imputation methods that introduce their own biases.
5. Potential for Misleading Interpretations: Simplified summaries can sometimes mask underlying complexities in the data, leading to misinterpretations or oversimplifications.

Assumptions of Descriptive Statistics:

1. Random Sampling: Many descriptive techniques assume that data is collected through random sampling to ensure that the sample is representative of the population.
2. Normal Distribution: Some methods (like parametric tests) assume that the data follows a normal distribution for accurate estimation of parameters such as mean and variance.
3. Independence of Observations: Descriptive statistics often assume that observations are independent of each other, especially in calculations of variance and covariance.

Considerations for Accurate Interpretation and Application:

1. Contextual Understanding: Always interpret descriptive statistics within the context of the problem domain and specific objectives of analysis.
2. Validation of Assumptions: Before applying any technique, validate assumptions such as data distribution, sample size adequacy, and absence of bias in data collection.
3. Use of Multiple Measures: Instead of relying on a single measure (e.g., mean), consider using multiple measures (median, range) to provide a more comprehensive view of the data.
4. Visualization for Insight: Complement numerical summaries with visualizations (like histograms, and box plots) to better understand the distribution and outliers in the data.
5. Robustness Checks: Perform sensitivity analyses or robust statistical methods to assess the stability of results against variations in assumptions or data characteristics.

Understanding the limitations, assumptions, and considerations of descriptive statistics is crucial for engineers to effectively analyze and interpret data. By acknowledging these factors and applying appropriate methods, engineers can derive meaningful insights that support informed decision-making and problem-solving in various applications.

Conclusion

Descriptive statistics form the bedrock of quantitative analysis, offering valuable insights into data characteristics through measures like central tendency, dispersion, and graphical representation. By summarizing key concepts and highlighting their significance, engineers can leverage these insights effectively in decision-making and research.

Summary of Key Concepts in Descriptive Statistics

Descriptive statistics encompasses measures that describe the central tendency, variability, and distribution of data. Key concepts include:

• Measures of Central Tendency: Such as mean, median, and mode, which provide a typical value around which data points cluster.
• Measures of Dispersion: Including range, variance, standard deviation, and interquartile range (IQR), which quantify the spread or dispersion of data points from the central value.
• Frequency Distributions: Representations of how often values occur within a dataset, visualized through histograms, frequency polygons, and cumulative frequency distributions.
• Graphical Methods: Tools like bar charts, pie charts, box plots, and scatter plots visually depict data relationships and distributions, aiding in intuitive understanding.
• Skewness and Kurtosis: Describe the shape and peak of data distributions, providing insights into asymmetry and tail behavior.
• Measures of Association: Such as covariance and correlation coefficient (Pearson correlation), which quantify the strength and direction of relationships between variables.

Importance of Descriptive Statistics in Decision-Making and Research

Descriptive statistics serve crucial roles in engineering contexts:

• Data Summarization: They condense large datasets into manageable summaries, facilitating easier interpretation and communication of findings.
• Pattern Recognition: By identifying trends, outliers, and patterns in data, descriptive statistics inform strategic decisions in engineering design, process optimization, and risk assessment.
• Baseline Establishment: Before delving into more complex analyses, descriptive statistics establish a foundational understanding of data characteristics, ensuring subsequent analyses are grounded in empirical insights.
• Comparative Analysis: They enable comparisons between different datasets or scenarios, supporting benchmarking, performance evaluation, and continuous improvement initiatives.

Practical Insight and Takeaways

Understanding descriptive statistics empowers engineers to:

• Interpret Data Effectively: By grasping how to calculate, interpret, and apply various statistical measures.
• Communicate Findings: Effectively convey insights to stakeholders through clear and insightful visualizations and summaries.
• Make Informed Decisions: Base decisions on data-driven insights that are grounded in robust statistical analysis.

By mastering descriptive statistics, engineers enhance their analytical capabilities, ensuring their contributions to projects and research are informed, accurate, and impactful.

To seize this opportunity, we need a program that empowers IT students with essential data science fundamentals, providing industry-ready skills aligned with academic pursuits at an affordable cost. Trizula Mastery in Data Science offers a self-paced, flexible program ensuring job readiness upon graduation. It covers contemporary technologies like AI, ML, NLP, and deep learning, laying a solid foundation for future advancement. Why wait? Click here to get started!

FAQs:

1. What is descriptive statistics in data science?

Descriptive statistics in data science involve summarizing and organizing data to make it understandable. This includes measures like mean, median, mode, and standard deviation to provide a clear picture of data characteristics and trends.

2. What are the 4 descriptive statistics?

The four key descriptive statistics are measures of central tendency (mean, median, mode), measures of variability (range, variance, standard deviation), measures of frequency (count, percent, frequency distribution), and measures of position (percentiles, quartiles).

3. What is descriptive analysis in data science?

Descriptive analysis in data science refers to the process of analyzing data sets to summarize their main characteristics. This often involves visual methods such as charts, graphs, and summary statistics to describe the basic features of the data.

4. What are descriptive statistics in science?

Descriptive statistics in science are used to summarize and describe the main features of a collection of data. They provide simple summaries about the sample and measures and form the basis for virtually every quantitative analysis of data.

5. What are the three main types of descriptive statistics?

The three main types of descriptive statistics are measures of central tendency (mean, median, mode), measures of dispersion (range, variance, standard deviation), and measures of frequency (frequency distributions, count, percentage)